Las cartas de
control son la herramienta más poderosa para analizar la variación en la
mayoría de los procesos.
Han sido difundidas exitosamente en varios
países dentro de una amplia variedad de situaciones para el control del proceso.
Las cartas de
control enfocan la atención hacia las causas especiales de variación cuando
estas aparecen y reflejan la magnitud de la variación debida a las causas
comunes.
Las causas
comunes o aleatorias se deben a la variación natural del proceso.
Las causas
especiales o atribuibles son por ejemplo: un mal ajuste de máquina, errores
del operador, defectos en materias primas.
Se dice que un
proceso está bajo Control Estadístico cuando presenta causas comunes
únicamente. Cuando ocurre esto tenemos un proceso estable y predecible.
Cuando existen causas especiales el proceso
está fuera de Control Estadístico; las gráficas de control detectan la
existencia de estas causas en el momento en que se dan, lo cual permite que
podamos tomar acciones al momento.
Ventajas:
·
Es una herramienta simple y efectiva
para lograr un control estadístico.
Cartas de control por variables y por atributos.-
En Control de Calidad mediante el término variable
se designa a cualquier característica de calidad “medible” tal como una
longitud, peso, temperatura, etc. Mientras que se denomina atributo a
las características de calidad que no son medibles y que presentan diferentes
estados tales como conforme y disconforme o defectuoso y no defectuoso.
Según sea el tipo de la característica de
calidad a controlar así será el correspondiente Gráfico de Control que, por
tanto, se clasifican en Cartas de Control por Variables y Cartas de Control por
Atributos.
Las cartas de control sirven para poder analizar el comportamiento de los diferentes procesos y poder prever posibles fallos de producción mediante métodos estadísticos. Estas se utilizan en la mayoría de los procesos industriales.
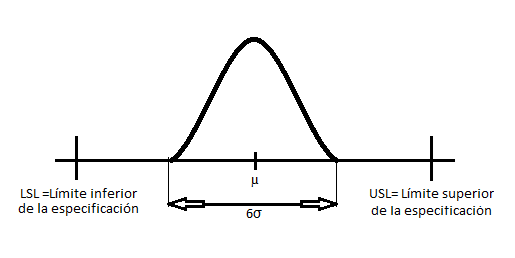
En ciertos procesos en los que se alcanza un alto grado de capacidad es aconsejable reducir el nivel de control proporcionado por las cartas de control estándar, para ello utilizaremos los límites de control modificados.
Los límites de control modificados para la Xmedia se utilizan cuando Cp o Cpk es mucho mayor que 1, es decir, cuando la variabilidad del proceso es mucho menor que la extensión de los límites. Pongamos, por ejemplo, que nuestro proceso consiste en llenar sacos de arena. Las especificaciones del fabricante exigen que cada saco sea llenado con una cantidad de arena entre los 10.00Kg y los 10.20 Kg. Por otra parte, nuestro proceso puede operar con una variación de 0.01 Kg. Vemos que en este caso la capacidad del proceso es:

En estos casos en los que el intervalo de las especificaciones es tan grande en relación a 6σ se recomienda cambiar de la carta de control de Xmedia habitual a la carta modificada. En esta, se permite el desplazamiento de la media un cierto rango, siempre que esta variación no resulte en la aparición de un número significativo de piezas defectuosas, es decir, producir piezas defectuosas con una probabilidad δ. La media se puede desplazar, tanto superior µU como inferiormente µL, un valor tal que la probabilidad de estar fuera de las especificaciones sea δ. Supondremos que la variabilidad del proceso está bajo control. Para especificar los nuevos límites de control de la carta modificada, tendremos en cuenta que el valor de la media tiene que estar entre µU y µL, se pueden calcular mediante:
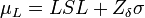
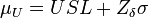
Donde Zδ representa el punto porcentual superior 100(1-α) de la distribución normal estándar.
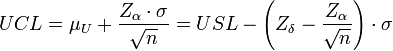

Para estimar estos límites lo más común es que la Zα tenga un valor de 3.
Para las cartas de control modificadas debe utilizarse una buena estimación de σ. En los casos en los que la variabilidad en el proceso cambia, los límites de control modificados no son adecuados y en su lugar se debe usar una carta R o S.
Las cartas de control se utilizan para chequear la estabilidad de un proceso. En
este contexto el proceso se dice que está bajo control estadístico si el o los parámetros
de la distribución de probabilidad de una característica de calidad bajo estudio,
permanecen invariables en el tiempo. Si un cambio se produce en alguno de ellos el
proceso se dice que está fuera de control.
Para monitorear la media de una característica de calidad normalmente
distribuida con la carta tradicional de observaciones individuales de Shewhart,
sucesivas muestras de tamaño n = 1 se obtienen a través del tiempo y se grafican
sobre la carta. El proceso se dice estar fuera de control cuando el valor graficado cae
fuera de los límites de control. Estos límites que se toman usualmente a ± 3σ de la
línea central, fijada en el valor de la media del proceso con desvío estándar igual a σ,
son conocidos como límites de control “ 3 - sigma".
Cuando se evalúa cuan efectiva es una carta de control para detectar cambios
en los parámetros de un proceso se pretende que los mismos sean detectados
inmediatamente después de que ocurra, que la tasa de falsa alarma sea baja y que la
tasa de muestreo sea razonable.
Una medida para la tasa promedio de muestreo se obtiene usando el número
promedio de observaciones hasta que se produce una señal. El número de
observaciones requeridas hasta una señal se denomina usualmente Longitud de
Corrida de la carta de control. El número promedio de observaciones que deben
graficarse antes de que una de ellas indique una condición fuera de control es la
Longitud de Corrida Promedio (LCP).Cuando el proceso está bajo control o cuando se
produce un cambio, la LCP puede evaluarse mediante cálculos probabilísticas.
Si bien una carta de control indica que el proceso está fuera de control cuando
un punto cae fuera de los límites de control, este suceso no es el único que puede
poner de manifiesto un desajuste del proceso. Es usual prestar atención a secuencias o
rachas que tengan poca posibilidad de ser observadas en un proceso bajo control y
cuando se adicionan a la carta reglas para detectar estas rachas no es sencillo
expresar a la LCP en términos de simples probabilidades.
En estos casos se suele utilizar un enfoque mediante el cual las cartas de control
se modelan como una cadena de Markov absorbente y a partir de las propiedades de
su matriz de transición evaluar la LCP.
En este trabajo hemos modelado mediante una cadena de Markov absorbente a la
carta de Shewhart para observaciones individuales adicionándole la regla de rachas :“2
de 3 puntos consecutivos más allá de los límites de advertencia 2 –sigma” a fin de
ilustrar este método para obtener la LCP.
Los límites de control modificados para la Xmedia se utilizan cuando Cp o Cpk es mucho mayor que 1, es decir, cuando la variabilidad del proceso es mucho menor que la extensión de los límites. Pongamos, por ejemplo, que nuestro proceso consiste en llenar sacos de arena. Las especificaciones del fabricante exigen que cada saco sea llenado con una cantidad de arena entre los 10.00Kg y los 10.20 Kg. Por otra parte, nuestro proceso puede operar con una variación de 0.01 Kg. Vemos que en este caso la capacidad del proceso es:

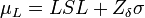
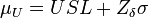
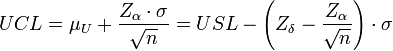

Para estimar estos límites lo más común es que la Zα tenga un valor de 3.


No hay comentarios.:
Publicar un comentario